簡単なA* （A star）経路探索アルゴリズム（Pythonコードつき）
はじめに
今日はA*経路探索（A star, エースター）アルゴリズムがどのようなプログラムかを実際のPythonコードで紹介します。
なぜA*なの？
プログラミングでゲーム開発などをしている人は、キャラクター(or 敵キャラクター）の経路探索（pathfinding)でA*を使いたいのではないでしょうか。
私はCodinGame（コーディングゲーム）というサイトで問題（テーマ）に沿ってコーディングしながらゲームチックに（グラフィカルにコーディング結果が反映される！）Pythonプログラミングを覚えていくのが好きなのですが、その中で「The Labyrinth」というpathfindingがテーマの問題に出会い、自力では限界を感じてアルゴリズムを検索した次第です。
https://www.codingame.com/training/hard/the-labyrinthところが！
私のプログラミングスキルではA*がよくわかりましぇ～ん！いろんなサイトを見ても微妙に書いてることが違ってたり、誤記があったりでなおさら理解が進まない。
ということで、お猿さんの自分へのやさしいイントロダクションとして、Pythonソースコード付きでこの記事を書いています。
A*のお勉強だ！
A*(A star:エースター）アルゴリズムとは
A*は経路探索アルゴリズムで、最短経路探索に優れていて、ヒューリスティック（ゴールまでの仮想距離を取り入れる）なアルゴリズムです（雑）。名前の由来は許容的 (英: Admissible)から来ているそうです。
あとはwikipediaに譲ります。
https://ja.wikipedia.org/wiki/A*A*アルゴリズムの解説
F = G + H
A*で最も重要なのはF=G+Hという考え方と、ノード(node)という考え方です。f, g, hという各変数があり、各ノード（迷路などでいうところの各ポジション）で計算されるものです。
- Fはあるノードでのトータルコスト（ここで言うコストとは移動距離と考える）。
- Gはスタートノードから現在ノードまでの距離（移動コスト）。
- Hは「ヒューリスティック」： 現在のノードからゴールノードまでの仮に見積もった距離。
ヒューリスティックとは「経験則的な」とか「試行錯誤的な」という意味です。
正確な距離が分かってたら答え出てるよね。仮に見積もった距離というのがA*のミソ
下図のrow（縦） × column（横） = 5×5の迷路を想定してA*を見ていきましょう。ここではスタート（Ｓ）が(0,0)、ゴール（Ｇ）が(4,4)とします。また、斜め移動は無しとし、タテ・ヨコ方向のみの移動が可能とします。
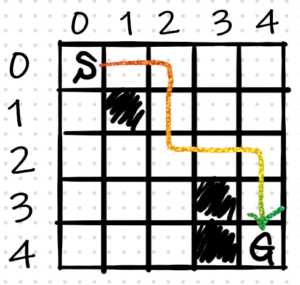
G
スタートノードから現在ノードまでの距離（移動コスト）
現在地点（現在ノード）がスタート地点(S)であればG=0、
右隣の(0,1)が現在地点であればG=1となります。
また、その下の(1,1)が現在地点であればG=2となります。下図のように赤矢印のルートに沿って１ずつGが増えていきます。簡単ですね。
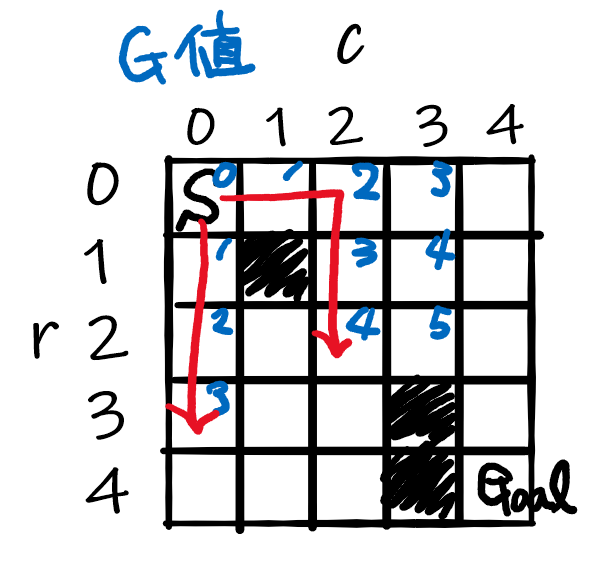
つまり、Gはスタート地点からの移動距離（1マスを距離１として）、言い換えると
移動先のG値は移動する1つ前のマスのG値＋1
G（node N) = G(N-1) + 1
となります。Gはサイトによって書いてあることが違い、あるサイトではGの計算を後ほど紹介するHと同様にx2+y2で表しているところもあり、要するにスタート地点から現在地点の距離が現わされれば良いようですね。
H
Hは現在のノードからゴールノードまでの仮に見積もった距離
次にHの距離を計算してみましょう。スタート地点（r=0, c=0)にいた場合、ゴールノードまでｒ方向に４つ、c方向に4つ移動する必要があります（障害物を無視して）。ピタゴラスの定理a2 + b2 = c2
に当てはめると、スタートノードのhは h = 42 + 42 = 32
です。
距離を求めるなら平方根（ルート）しなくちゃいけないのでは？
ルートする必要はないんだ。2乗のままで比較して良いぞ。ルートしてもいいけどしなくても同じ結果のようだぞ！計算例を下図に示すぞ。
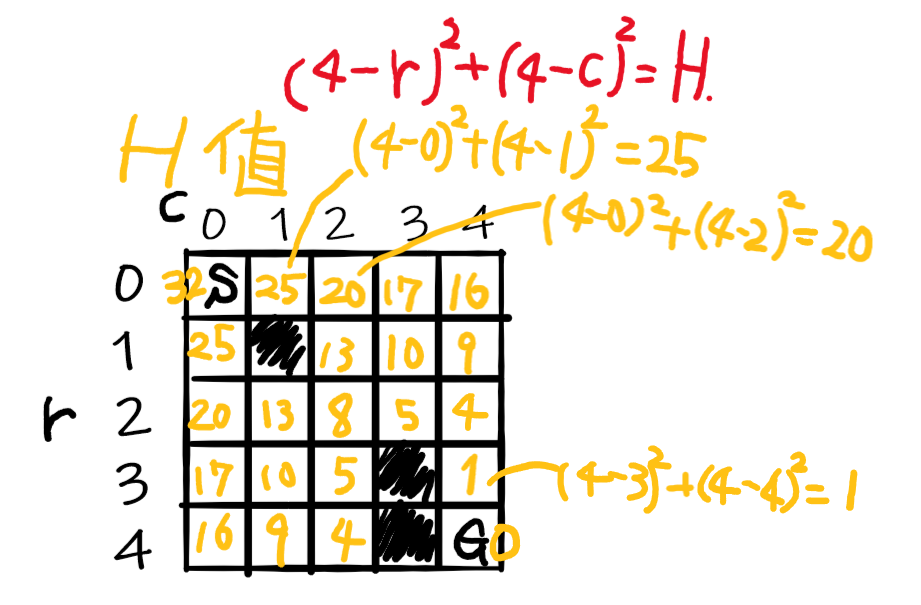
H = (Goal_r – r )2 + (Goal_c – c )2
ゴール地点（ Goal_r, Goal_c )、 現在地点（ r, c )
F
あるノードでのトータルコスト（G+H)
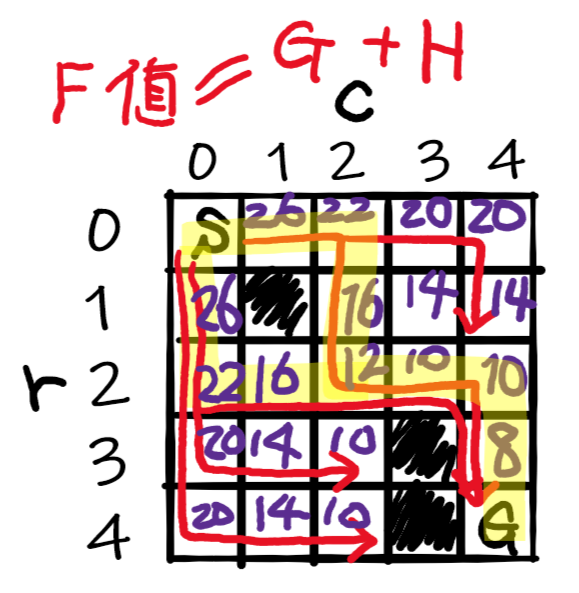
HとGを足してあるノードでのトータルコストFを計算しよう。例えばスタート地点(0,0)から右隣りの(0,1)に移動する場合のF値は F = G + H = 1 + 25 = 27 です。
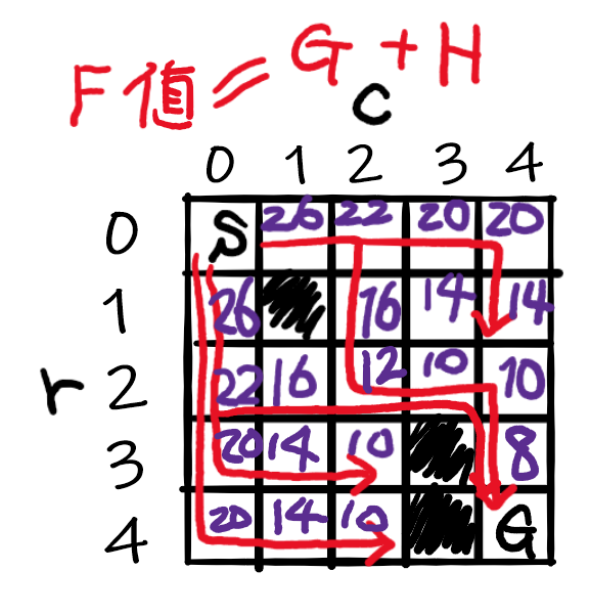
F = G + Hの使い方
F、G、Hの計算は分かったけど、結局それをどう使えばいいの？
現在位置から移動可能な候補のみに絞ってFを計算し、候補のうち一番小さいFの位置（現時点で最もゴールに近い）へ移動。これを繰り返すんだ！全部のマスを計算する必要はない！
A*の考え方
A*はヒューリスティック関数のH計算により、基本的には現在地点からゴール方向に突き進もう（Fが一番小さい）とします。Fが小さいルートを選んで突き進んだ結果、迷路の行き止まりにぶち当たることもあるでしょう。そういった場合、行き止まりルートは除外して、Fが次に小さいルートで突き進むことを繰り返します。このヒューリスティックの計算により、すべてのルートを枝分かれしてくまなく計算していくより、断然に早く最短ルートを見つけられる仕組みになっています。
A*の実装
A*のプログラム的考え方
まずは、A*アルゴリズム（プログラム）のソースコードなしの概念（考え方）を見ていきましょう。
- スタートノードをオープンリストに追加する。
- 下記手順を繰り返す。
- オープンリストの中で最も低いF値を探してください。これを現在のノードとします。
- これをオープンリストから削除し、クローズリストに追加してください。
- 現在ノードに対して移動可能な4方向ノード（上下左右）、斜め移動をＯＫとするなら8方向ノード（上下左右＋斜め4方向）の子ノードに対し、
- 移動不可能位置 or クローズリストにあるなら無視、それ以外なら次の手順を実行
- オープンリストになければ追加する。その際現在ノードを子ノードの親に設定する。そして子ノードのF,G,H値を計算する。
- オープンリストに同じ子ノード（同じ位置）が既にあれば、G値を比較してより良い経路かどうか（G値が小さいかどうか）確認する。小さいG値はより良い経路を意味します。もし、同じ子ノードでより小さいG値であれば、親ノードを現在ノードに設定する。
- もし次を満たすならプログラム終了する。
- 現在ノードがゴールノードだったら（ゴールを見つけたら）、
- 又はゴールノードが見つからず、オープンリストが空っぽになったら。（ゴールへの経路が存在しないケース。）
- 見つけた経路を保存する。ゴールノードの親ノードを辿っていき、スタートノードに戻るまで親を辿っていく。各ノード位置を逆順(reverse)にすると欲しい経路が出るよ。
A*の実装（Pythonソースコード）
では、実際のソースコードをご確認下さい。
やったね！あとはnode クラスとastar関数を自分のプロジェクトにコピペするだけで使えるよ！
# A* (A-star)経路探索プログラム
class Node():
"""A node class for A* Pathfinding"""
def __init__(self, parent=None, position=None):
self.parent = parent # 親ノードの設定
self.position = position # (row, column)のタプル ※row：行、column：列
self.g = 0
self.h = 0
self.f = 0
def __eq__(self, other):
# node 同士の比較演算子(==)を使用できるように
return self.position == other.position
def astar(maze, start, end):
"""Returns a list of tuples as a path from the given start to the given end in the given maze"""
# maze: 迷路リスト、start:スタートポジション、end:ゴールポジション
# ゴールまでの最短経路のリストを返す関数
# Create start and end node
# スタート、エンド（ゴール）ノードの初期化
start_node = Node(None, start) # 親ノードは無し
start_node.g = start_node.h = start_node.f = 0
end_node = Node(None, end)
end_node.g = end_node.h = end_node.f = 0
# Initialize both open and closed list
open_list = [] # 経路候補を入れとくリスト
closed_list = [] # 計算終わった用済みリスト
# Add the start node
# 経路候補にスタートノードを追加して計算スタート
open_list.append(start_node)
# Loop until you find the end
while len(open_list) > 0:
# Get the current node
current_node = open_list[0]
current_index = 0
for index, item in enumerate(open_list):
# オープンリストの中でF値が一番小さいノードを選ぶ
if item.f < current_node.f:
current_node = item
current_index = index
# Pop current off open list, add to closed list
# 一番小さいF値のノードをオープンリストから削除して、クローズリストに追加
open_list.pop(current_index)
closed_list.append(current_node)
# Found the goal
# ゴールに到達してれば経路(Path)を表示して終了
if current_node == end_node:
path = []
current = current_node
while current is not None:
path.append(current.position)
current = current.parent
return path[::-1] # Return reversed path
# Generate children
# ゴールに到達してなければ子ノードを生成
children = []
# for new_position in [(0, -1), (0, 1), (-1, 0), (1, 0), (-1, -1), (-1, 1), (1, -1), (1, 1)]: # 斜め移動ありの場合
for new_position in [(0, -1), (0, 1), (-1, 0), (1, 0)]: # 上下左右移動のみ (Adjacent squares
# Get node position
node_position = (current_node.position[0] + new_position[0], current_node.position[1] + new_position[1])
# Make sure within range
# 迷路内の移動に限る
if node_position[0] > (len(maze) - 1) or node_position[0] < 0 or node_position[1] > (len(maze[len(maze)-1]) -1) or node_position[1] < 0:
continue
# Make sure walkable terrain
# 移動できる位置に限る（障害物は移動できない）
if maze[node_position[0]][node_position[1]] != 0:
continue
# Create new node
# 移動できる位置のノードのみを生成
new_node = Node(current_node, node_position)
# Append
# 子リストに追加
children.append(new_node)
# Loop through children
# 各子ノードでG, H, Fを計算
for child in children:
# Child is on the closed list
if len([closed_child for closed_child in closed_list if closed_child == child]) > 0:
continue
# Create the f, g, and h values
# G は親ノード + 1
child.g = current_node.g + 1
# H は （現在位置 - エンド位置)の2乗
child.h = ((child.position[0] - end_node.position[0]) ** 2) + ((child.position[1] - end_node.position[1]) ** 2)
# F = G + H
child.f = child.g + child.h
# Child is already in the open list
if len([open_node for open_node in open_list if child.position == open_node.position and child.g > open_node.g]) > 0:
continue
# Add the child to the open list
# 子ノードをオープンリストに追加
open_list.append(child)
def example():
maze = [[0, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0]]
start = (0, 0)
end = (4, 4)
path = astar(maze, start, end)
print(path)
if __name__ == '__main__':
example()
# A*で見つけたパス
# [(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 3), (2, 4), (3, 4), (4, 4)]いじわる迷路でテスト
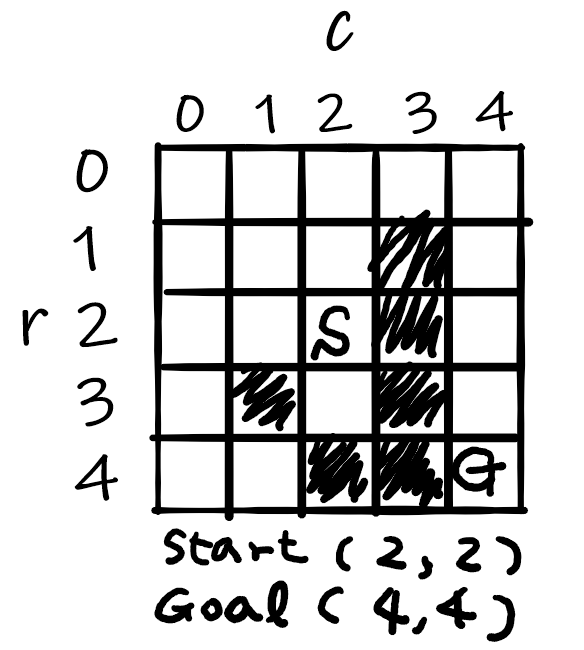
下図のようなスタート（2,2)→ゴール(4,4)で間に壁があり、遠回りしないとゴールできないようないじわる迷路マップでテストしてみましょう。ヒューリスティック関数Hはゴールに近づこうとするので、遠回り（正解ルート）する過程を見ていきます。
なお、ソースコードは下記のexample()部分を書き換えるだけでOKです。
# いじわる迷路版でテスト
def example():
maze = [[0, 0, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 1, 0],
[0, 0, 1, 1, 0]]
start = (2, 2)
end = (4, 4)
path = astar(maze, start, end)
print(path)
# [(2, 2), (1, 2), (0, 2), (0, 3), (0, 4), (1, 4), (2, 4), (3, 4), (4, 4)]
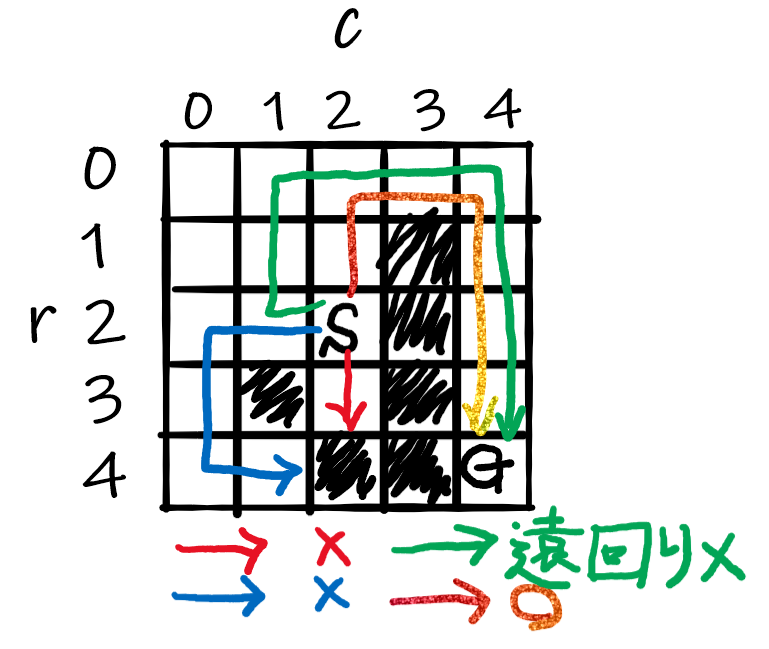
汚い手書きでごめんなさい！
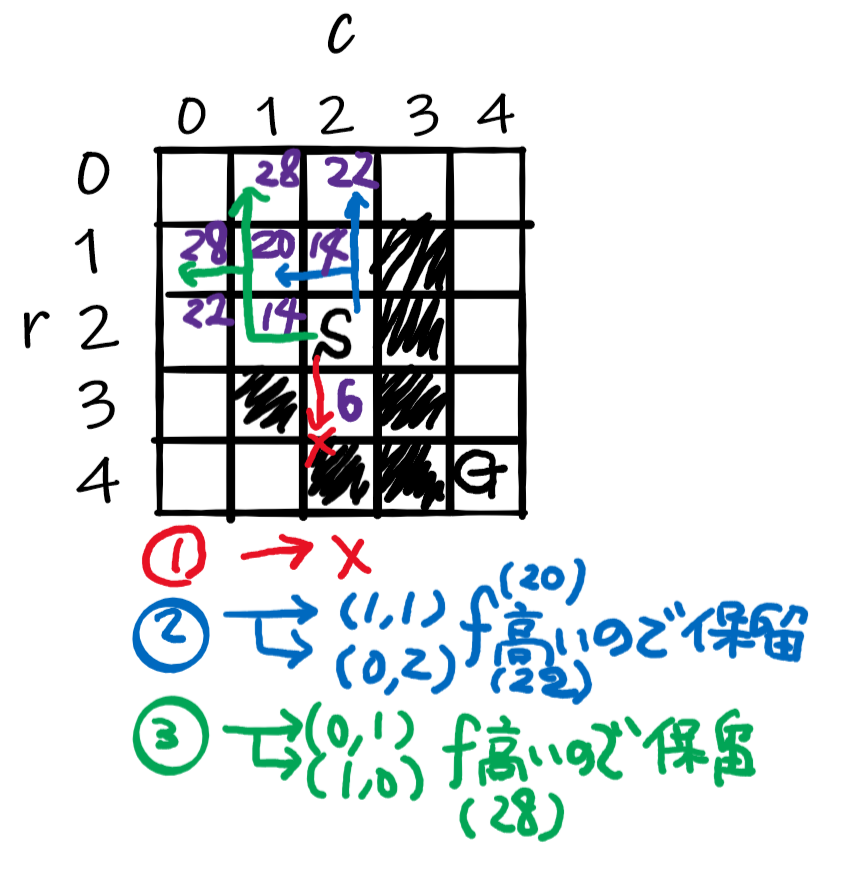
上手のマップを見ながら読んでください。
- まず、予想通りゴールに物理的に近づく真下(3,2)へ行きました。このときF＝６で最小。ただし、その先は完全に行き止まりの為、子ノードは発生しません。
- 次にF値が低かったところに戻ります。F＝14が2つあったのでどちらでも良いのですが、まず真上(1,2)を選択。
- 子ノードがさらにその上（0,2)のF=22と、(1,1) のF=20ですが、先ほど計算したF=14で選ばなかった左（2,1)の方が小さいので（F=14と20 or 22)保留にし、F=14 (2,1)に戻ります。
- F = 14 (2,1)に戻り、子ノードは(1,1)のF=20と、(2,0)のF=22の為、(1,1)を選択。
- さらに(1,1)の子ノードは(0,1)のF=28と、(1,0)のF=28に。先ほど計算した(2,0)のF=22の方が小さいので子ノードを深く見ていくのを中断（保留）して、(2,0)に戻ります。
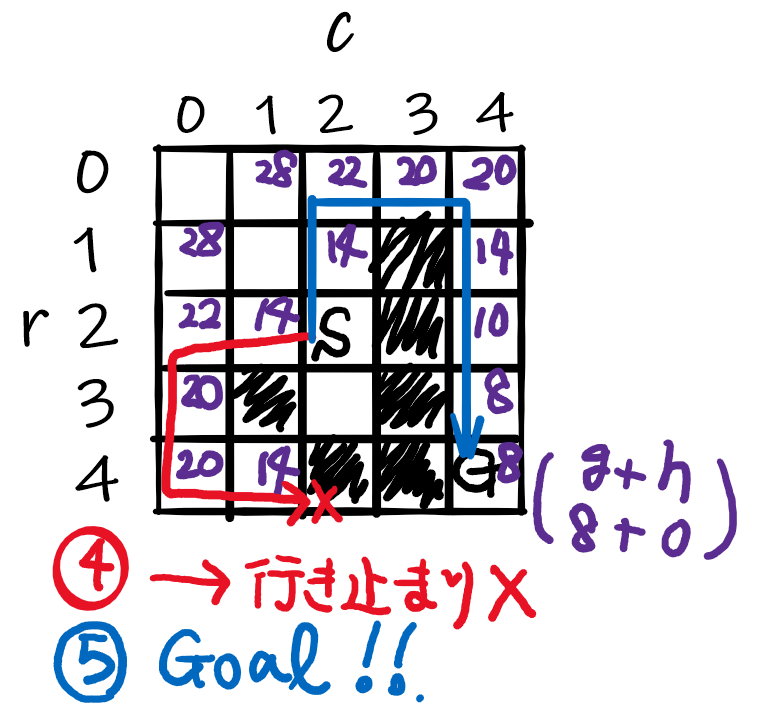
- (2,0) F= 22に戻りまして、同様に子ノードを辿っていくと、(2,0) → (3,0) → (4,0) → (4,1)F=14まで来ましたが、残念！行き止まりでした。
- 現時点で計算済みや行き止まりと判明した位置はクローズドリストに移動されており、オープンリストに残っているのは先ほど中断（保留）していた、(0,2) F=22、(0,1)と(1,0)どちらもF=28、の為、スタート地点の上の上である(0,2)F=22に戻りましょう。
- (0,2)に戻り、左(0,1)行くか・右(0,2)行くかですが、F値が一番小さい(F=20)右に行きます。
- その後は1本道なので省略しますが、ゴールまで順調にF値が小さくなっていくことが分かります。
- ちなみにゴール(4,4)のF値は0になりません。H値（ヒューリスティック）が0になるだけで、G値（移動距離）が残ります。この場合、ゴールまで最短で8回移動で到達できるのでG=8、H=0となり、F＝８となりました。
A*（Aスター）アルゴリズムの理解が出来ましたでしょうか。参考になれば幸いです。
参考サイト
下記サイト（英語）を大いに参考にさせて頂きました。オリジナルソースコード、改良版も載っていますので是非ご確認ください。
https://medium.com/@nicholas.w.swift/easy-a-star-pathfinding...
Python 初心者
しがない会社員が日曜プログラミングを趣味として楽しんでいます。
CodinGame（https://www.codingame.com/）でゲームチックにプログラミングしながらPythonの基礎を覚えるスタイル。覚えたことをブログにしていければと。
ソースコードエディターはVisual Studio Code を愛用。
当サイトについて